Geometry Special Right Triangles 30 60 90 Worksheet Answers Properties of a 30 176 60 176 90 176 Triangle One angle is 30 176 one angle is 60 176 and one angle is 90 176 The length of the adjacent is 3 215 opposite The length of the hypotenuse is 2 215 opposite
Problem 1 What is the value of z in the triangle below Don t use the Pythagorean theorem Use the properties of special right triangles described on this page Right Triangle Calculator Special Right Triangles 30 60 90 and 45 45 90 triangles explained with formulas examples and pictures Oct 5 2021 0183 32 Special Right Triangles 30 60 90 Practice pwelch Member for 3 years 5 months Age 13 18 Level 9 12 Language English en ID 986875 10 05 2021 Country code US Country United States School subject Math 1061955 Main content Tria 1372307 Special Right Triangles 30 60 90 Practice Loading ad Share Print Worksheet Finish
Geometry Special Right Triangles 30 60 90 Worksheet Answers
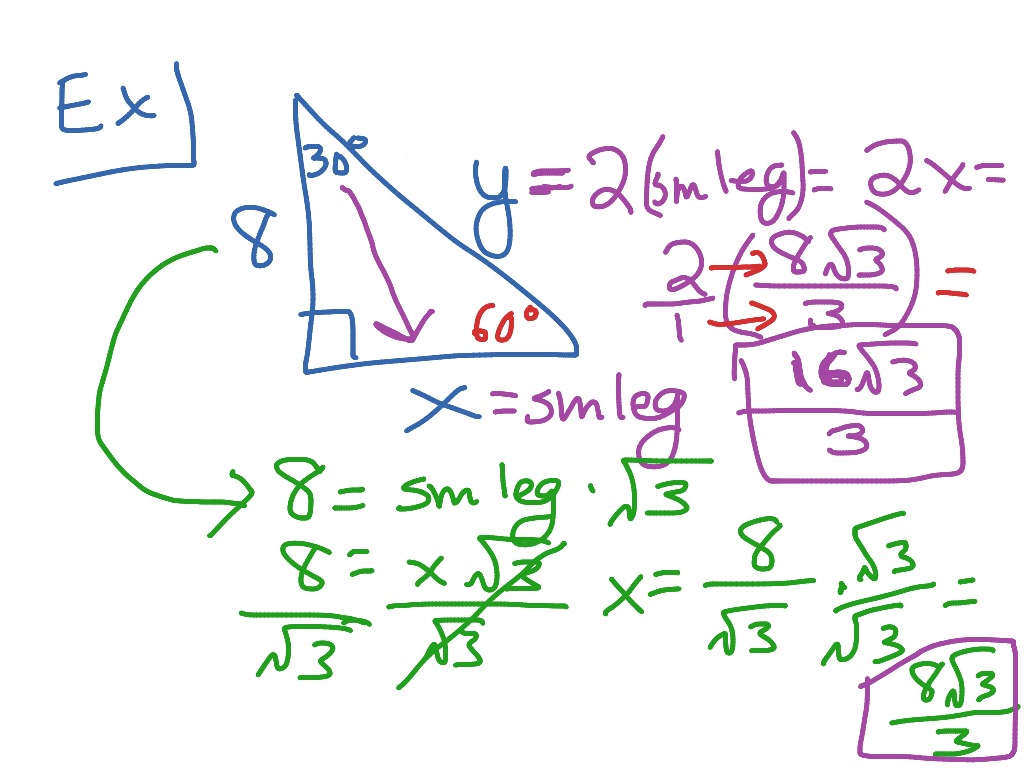 Geometry Special Right Triangles 30 60 90 Worksheet Answers
Geometry Special Right Triangles 30 60 90 Worksheet Answers
https://showme0-9071.kxcdn.com/files/77172/pictures/thumbs/735939/last_thumb1361914727.jpg
Practice 30 60 90 Triangle A 30 60 90 triangle is a special right angled triangle as the angles of the triangle are in the ratio 1 2 3 There are different types of triangles such as obtuse isosceles acute equilateral and so on But only a few types of triangles are considered special triangles
Templates are pre-designed files or files that can be used for numerous functions. They can conserve effort and time by providing a ready-made format and design for creating different kinds of material. Templates can be used for personal or expert jobs, such as resumes, invites, leaflets, newsletters, reports, discussions, and more.
Geometry Special Right Triangles 30 60 90 Worksheet Answers
Right Triangle Geometry Viewing Gallery

50 30 60 90 Triangles Worksheet

Special Right Triangles Interactive Notebook Page Teaching Geometry
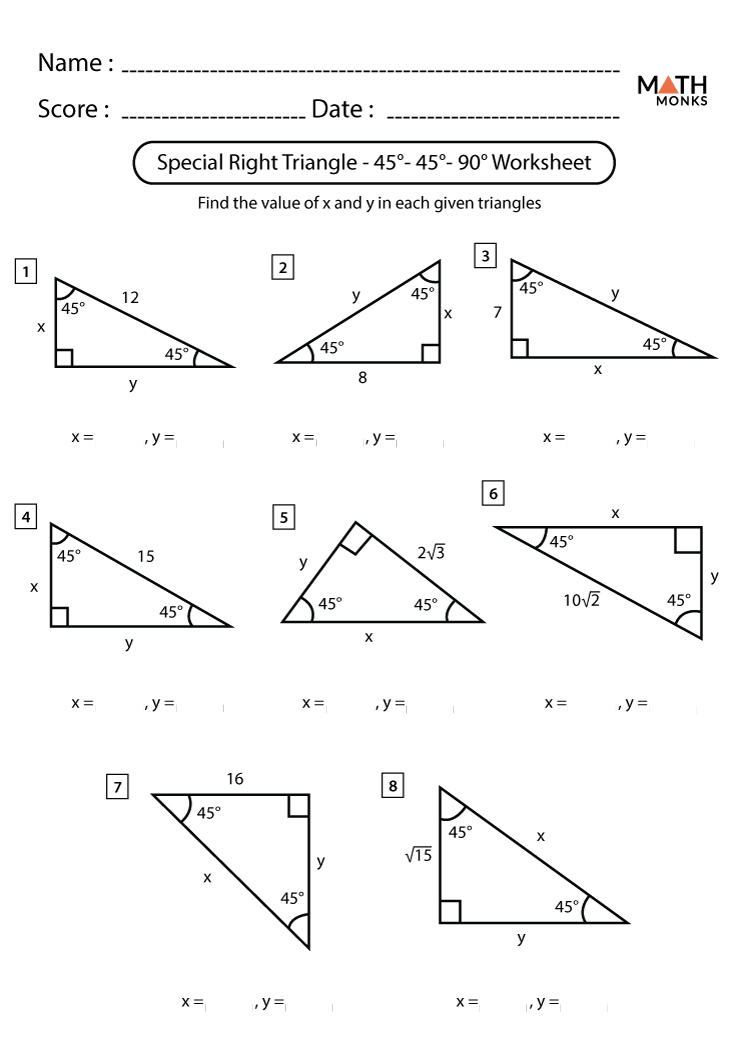
Special Right Triangles Worksheets Math Monks

Applying Special Right Triangles Lesson Plan For 10th Grade Lesson Planet
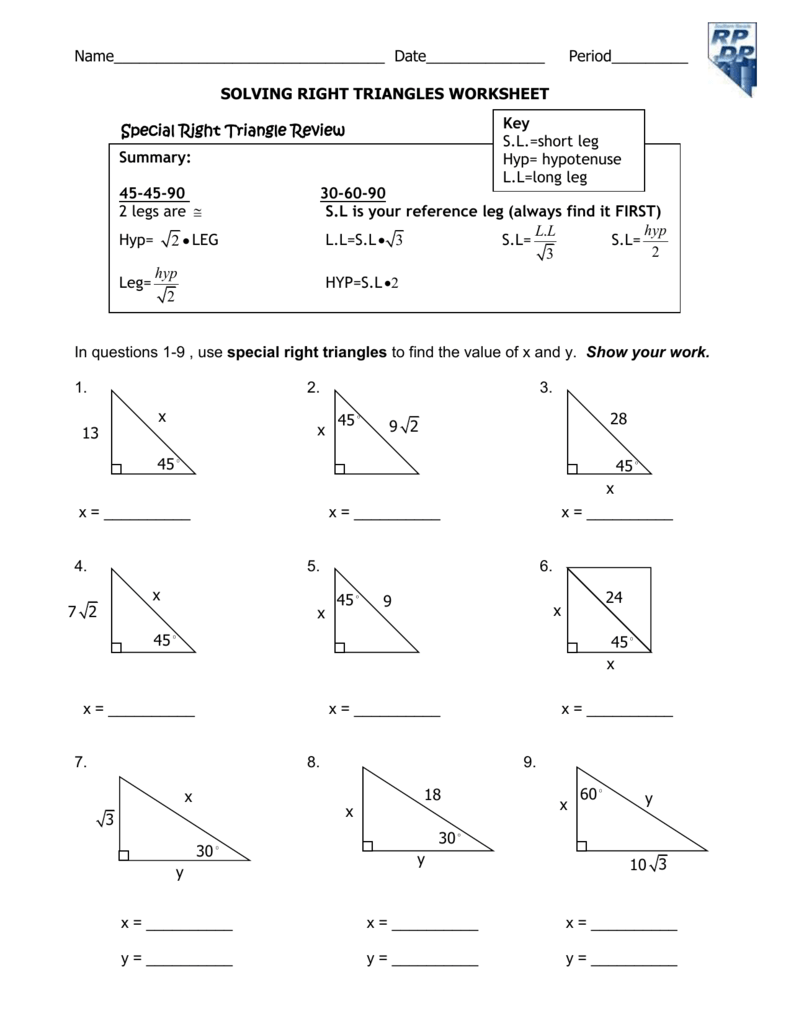
Right Triangle Trigonometry Worksheet Answers

https://www.khanacademy.org/math/geometry/hs-geo
I use this trick on 30 60 90 triangles and I ve never gotten a single wrong 1 The small leg to the hypotenuse is times 2 Hypotenuse to the small leg is divided by 2 2 The small leg x to the longer leg is x radical three For Example Pretend that the short leg is 4 and we will represent that as quot x quot

https://matterofmath.com/geometry/special-right-triangles
They are called 45 45 90 triangles and 30 60 90 triangles In this lesson there is a free printable worksheet an explanation of what makes these triangles special how to spot them and what you can do to find out more about one that s in front of you using the Pythagorean Theorem and trigonometry SOH CAH TOA
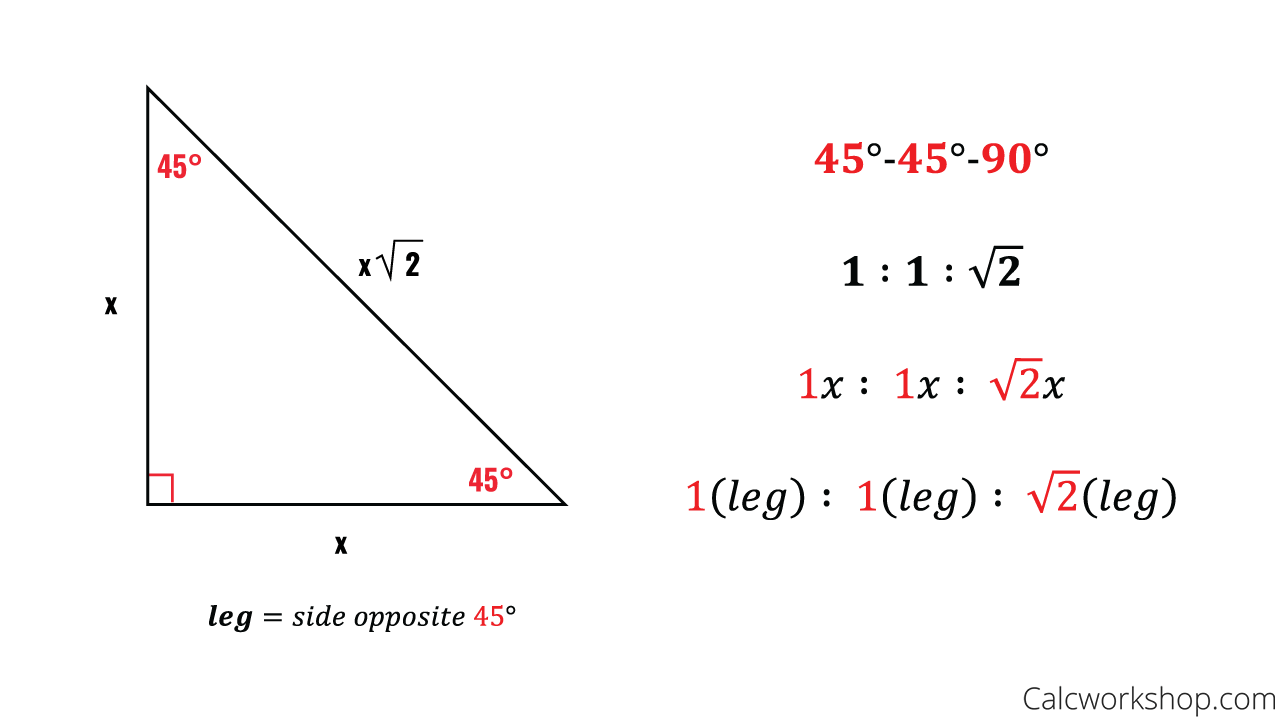
https://mathmonks.com/worksheets/special-right-triangles-worksheets
Special Right Triangles Worksheets Special right triangles are the focus of the below printables Know the Pythagora s theorem like the back of your hand for nailing these sums

https://brighterly.com/worksheets/30-60-90-triangle-worksheets
Jan 25 2023 0183 32 A 30 60 90 triangle is a special kind of triangle that has three sides and three angles Two of the angles are the same but the third one is different in a 30 60 90 triangle the three sides are always in the ratio of 1 sqrt 3 2 and the three angles are always 30 60 90

https://www.onlinemathlearning.com/30-60-90.html
A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore if we are given one side we are able to easily find the other sides using the ratio of 1 2 3
Solution Step 1 Test the ratio of the lengths to see if it fits the n n 3 2n ratio 4 4 3 n n 3 2n Step 2 Yes it is a 30 60 90 triangle with n 4 Step 3 Calculate the third side 2 n 2 215 4 8 Answer The length of the hypotenuse is 8 inches You can also recognize a 30 60 90 triangle by the angles Course High school geometry gt Unit 5 Lesson 3 Special right triangles Special right triangles proof part 1 Special right triangles proof part 2 Special right triangles 30 60 90 triangle example problem Area of a regular hexagon
1 A right triangle has a 60 degree angle and the leg adjacent to that angle has a length of 7 in Find the length of the other leg 2 A right triangle has a 45 degree angle and the hypotenuse has a length of 8 ft Find the length of a leg 3 The hypotenuse of a right triangle with a 30 degree angle has a length of 9 cm